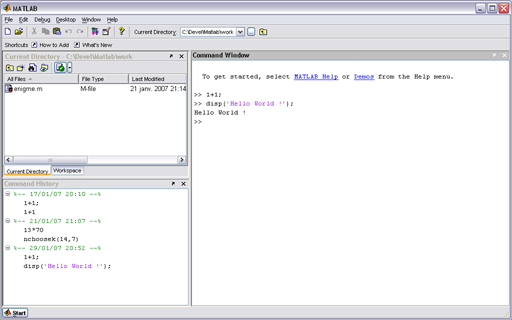
Voilà l'interface typique que l'on obtient sous Windows XP avec Matlab 7 : Décrivons les différentes zones :

• Barre d'outils : peu souvent utilisée et intuitive de toute manière
• Current Directory : liste tous les fichiers présents dans le répertoire courant (qui est par défaut $MATLAB_DIR$\work). C'est là où il faut mettre tous les fichiers M que l'on voudra utiliser : ici il n'y a qu'un fichier, qui se trouve être un fichier M nommé énigme.
• Workspace (visible dans la même zone en cliquant sur l'onglet) : liste toutes les variables définies, leurs valeurs et leur type. Utile lors de débuggage.
• Command history : no comment
• Command window : Sorte de console où apparaissent les résultats des fichiers M, où doivent être tapées les commandes en mode interactif …

• Rendons-nous dans la fenêtre principale pour taper :

x=1+2;

A priori, rien ne s'est passé, rien n'est affiché. Mais en regardant l'onglet Workspace, on se rend compte qu'une nouvelle variable (ici x) est créée. Pour afficher le contenu d'une variable dans la command window, il suffit de taper le nom de la variable sans point-virgule final :

x

Si on avait voulu simplement afficher le résultat d'une opération sans créer de variable, il suffit de taper l'expression à calculer sans point-virgule :

18.02-29.01

Dans ce cas où aucune variable n'est spécifiée, le résultat du calcul est par défaut enregistré dans une variable nommée ans.

• Les priorités des opérateurs sont classiques :

19.84E2/2^6

renverra le résultat de (19.84*(10^2)) / (2^6).

• Les nombres complexes peuvent se noter soit avec la notation i ou j :

(1+i)*(1-j)

Cependant, attention : une fois que la variable i est utilisée (dans les boucles par exemples), elle ne peut plus être ensuite utilisée pour son sens i^2=-1. Il est donc préconisé de se définir des règles du genre : je m'interdis le nom j pour les variables (que j'utiliserai pour les complexes), mais je pourrai utiliser la lettre i dans les boucles, …

• Enfin, les fonctions trigonométriques s'utilisent sans problème (à noter la variable pi prédéfinie) :

sin(pi/2)

On va commencer en douceur pour éviter les clacages :

1. Calculer le cosinus de Pi/3
2. Enregistrer dans une variable nommée z la valeur de cos²+sin² en Pi/5, puis vérifier la valeur de z en l'affichant
3. Si tout s'est bien passé, on peut faire des choses plus rigolotes : Leçon 2 : Manipuler les vecteurs